数据建模分析中数据统计关系常见类型与示例
2023-12-06 19:09:44
次
本文介绍4种数据统计关系常见类型：
1、单变量数据探索
可以使用描述数据特征节点对连续型或离散型数据的中心分布趋势和变量的分布进行探索。对于连续型数据，在洞察-模型【数值型变量统计信息】表格中进行各指标的查看；对于离散型数据，在洞察-模型【字符或日期型变量统计信息】表格中进行各变量计数和占比统计信息的查看。
2、两变量之间关系
可以使用散点图、圆饼图、分组折线图、相关系数和方差分析节点进行分析。
散点图用于描述两个数值型变量之间关系。
圆饼图用于描述一个字符型变量和一个数值型变量之间关系，按照某个分类变量显示某分析变量的每一个数值相对于总数值的大小，其大小通过圆中的扇面来衡量。
分组折线图是折线图衍生图。当不选择分组变量时，可以用来显示随着时间（如日、月、年度）而变化的连续型数据。
相关系数节点支持相关系数选择和方差膨胀因子的计算方法。相关系数的取值一般介于-1和1之间。当相关系数为正时，意味着变量之间是正相关；当相关系数为负时，意味着变量之间是负相关。方差膨胀因子表示变量之间复共性程度的数值。
方差分析节点仅针对单因素方差分析，用于判断一个因素对另一个因素是否存在显著性影响，因变量为分析因素，类型为数值型，因子为影响因素，可为数值型或字符型，最终可通过洞察中图表或结果数据集中的P值进行判断，P<0.05，表示因子的取值对因变量影响显著。方差分析节点需要注意的是需要因子各类别样本数不小于2，否则会运行失败。
3、多变量之间关系
可以使用条线图、散点图矩阵、平行坐标图、分组折线图、分组散点图、分组柱状图、相关系数、偏相关分析和概率单位回归节点进行分析。
条线图将柱形图图表与线型图图表组合起来绘制在一个图表中。描述一个字符型与两个数值型变量之间关系。
散点图矩阵是散点图的高维扩展，它从一定程度上克服了在平面上展示高维数据的困难。散点图矩阵支持同时看到多个单独变量的分布和它们两两之间的关系。
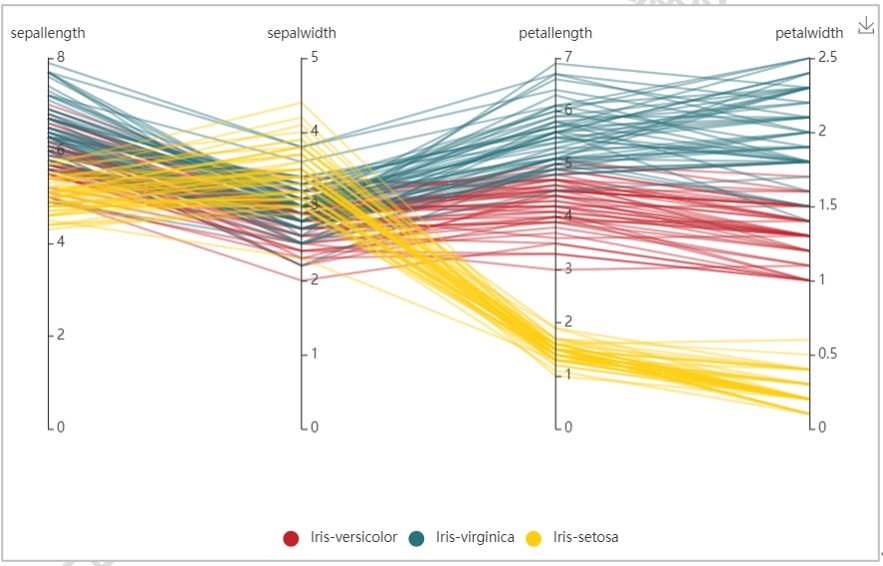
平行坐标图用于描述一个字符型变量和两个及两个以上数值型变量之间关系，将高维数据的各个变量用一系列相互平行的坐标轴表示，以样例数据中的Iris_Cluster为例，分组变量选择label，分析变量选择sepallength、sepalwidth、petallength和petalwidth，结果如下图：
分组折线图当对分组变量进行选择后，可以用来描述不同分类变量下，数值型变量随时间变化趋势。
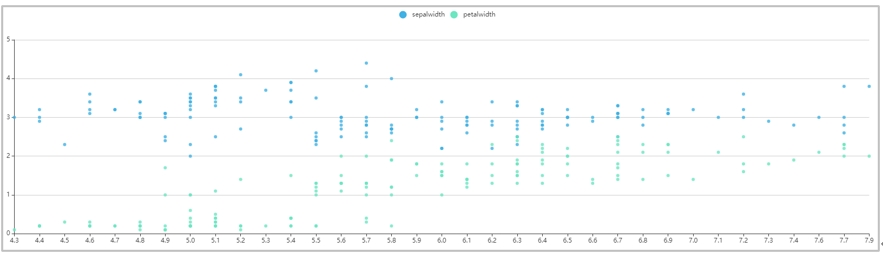
分组散点图是散点图的一种扩充展示图，反映在分组变量下两个变量之间的数据值关系和变化趋势。分组散点图在散点图的基础上增加了分组变量，比散点图表达的信息更多。分组散点图有两种使用场景，一种是选择多个Y轴字段，分组字段不可选的情况，那么就会将Y轴的每个字段的数据当作一个分组进行散点图展示，以样例数据中的Iris_Cluster为例X轴字段选择sepallength，Y轴字段选择sepalwidth和petalwidth进行画图，结果如下图：
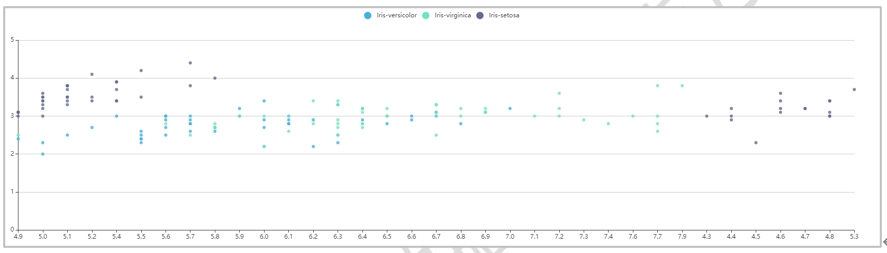
另一种场景是只选择了一个Y轴字段，并且选择了一个字符类型的字段作为分组字段，那么将会按照分组字段去进行散点图分组展示，以样例数据中的Iris_Cluster为例X轴字段选择sepallength，Y轴字段选择sepalwidth，分组字段选择label，结果如下图：
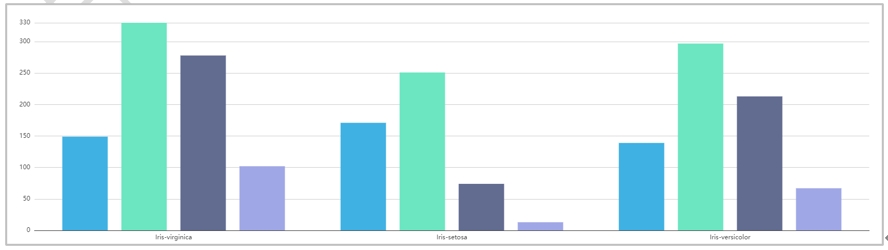
分组柱状图通过在图变量的不同值之间比较数值或统计量来创建垂直、水平的分组柱状图。分组柱状图通过将条显示为不同高度来展示数据的相对量值。每个条代表一类数据。分组柱状图也有两种使用场景，一种是选择多个Y轴字段，分组字段不可选的情况，那么就会将Y轴的每个字段当作一个分组进行柱状图展示（不同颜色表示不同分组），以样例数据中的Iris_Cluster为例X轴字段选择label，Y轴字段选择sepallength、sepalwidth、petallength和petalwidth进行画图，结果如下图：
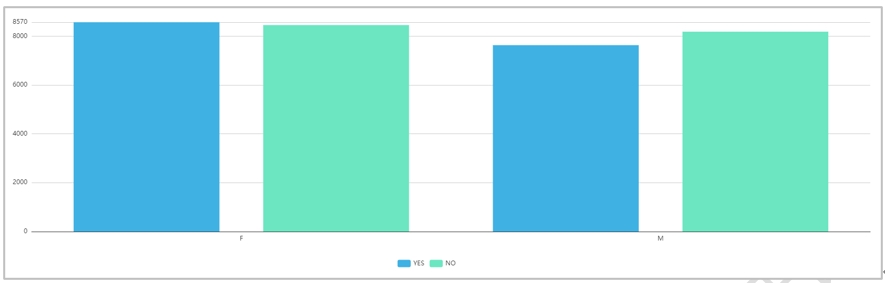
另一种场景是只选择了一个Y轴字段，并且选择了一个字符类型的字段作为分组字段，那么将会按照分组字段去进行柱状图分组展示（不同颜色表示不同分组），以样例数据中的Baskets_Association为例X轴字段选择sex，Y轴字段选择age，分组字段选择homeown，结果如下图：
偏相关分析用于当两个变量同时与第三个变量相关时，将第三个变量的影响剔除，只分析另外两个变量之间相关程度的情况。其中待分析的相关变量可以选择多个，控制变量可以选择一个或两个。
概率单位回归是将概率转换为与自变量所对应的标准正态离差，将因变量反应率P转换为单位概率，然后和协变量建立回归关系，即完成了概率单位回归方程构建。其中，协变量、观测值汇总及响应频率均为数值型变量，协变量变换方式包括“无”、“ln”、“log10”。
4、两组变量/数据之间关系
可以使用典型相关分析和相似度节点进行分析。
典型相关分析节点针对一个数据集中的两组变量进行分析，借用主成分分析降维的思想，分别对两组变量提取主成分，且使两组变量提取的主成分之间的相关程度达到最大，而从同一组内部提取的各主成分之间互不相关，用从两组之间分别提取的主成分的相关性来描述两组变量整体的线性相关关系。
相似度节点针对两组数据公共字段进行每行数据之间的距离计算从而衡量对象之间的相似程度。支持欧式距离、曼哈顿距离、余弦距离和Tanimoto距离进行对象的相似度计算，并且可指定输出的相似文档个数。
Tempo商业智能平台
Tempo人工智能平台
Tempo数据工厂平台
Tempo指标平台
Tempo数据治理平台
Tempo主数据管理平台
首页
陕公网安备 61019002000171号
